Sharing Sensors with OEM Controllers

A. Yes, it can sometimes be done, and this is how:

Sensors that have a voltage output (EGO O2 sensors, throttle position sensors (TPS), manifold absolute pressure (MAP) sensors, VR and Hall ignition/crank/cam sensors, and many mass air flow (MAF) sensors) have a variable voltage signal that can be tapped into and used directly by your MegaSquirt^® controllers high-impedance inputs (high impedance means they won't draw much current) without affecting the OEM ECU.

Sensors that have a varying resistance response require bias voltages through a bias resistor, and there must only be one bias resistor per sensor at any given time. Temperature sensors are typically negative temperature coefficient (NTC) thermistors (i.e. variable resistance that decreases with increasing temperature). So if you wish to share temperature sensors between your OEM ECU and your MegaSquirt^® controller, you need to eliminate the MegaSquirt^® controller bias resistor, and determine the value of the OEM ECU's bias resistor. You can do this as follows:

• First, you must remove the 2.49k bias resistors on the MegaSquirt^® EFI Controller, R4 (IAT) & R7 (CLT). You do not jumper them, or replace them with other resistors, simply leave them out.
• Next, you need to determine the stock computer's bias resistor. This can be tricky because some ECUs (GM for example) have 2 bias resistors and swap them in at different temperatures to gain accuracy. Example, -40°F to +40°F and +40°F to 230°F. If your ECU does this, you can't easily hookup the MegaSquirt^® in parallel.
• If your ECU uses a single bias resistor, then it should work well with your MegaSquirt^® EFI controller. If your OEM ECU uses two bias resistors, you could configure the MegaSquirt^® for the 'hot' bias value and just accept what behavior the 'cold' bias value will cause. Alternatively, you can always install separate IAT and CLT sensors for your MegaSquirt^® EFI controller to use.

  Here is how to determine if you have 1 or 2 bias resistors per sensor and what their resistance values are:

  First, the sensor and bias resistor act as a voltage divider. Each of the two resistors drop voltage in proportion to their resistance. The voltage were are interested in is the voltage between the two resistors (bias and sensor). The equation is:
  V_o = V_i / (R₁ + R₂) / R₂

  Or:

  Output equals the bias voltage divided by the ratio of the sum of the combined resistances divided by the sensor resistance.

  The bias voltage is almost always 5.00 volts for any EFI system you will encounter.

  There is 5.00 volts applied to one end of the bias resistor, and the temperature sensor (aka 'thermistor') is connected from ground to the other end of the bias resistor. The ECU reads the voltage at the junction of the bias resistor and the temperature sensor to determine its resistance value (and thus the temperature).

  This equation can be used to find the variable resistance value in a voltage divider:

  R_o = R_b × V_o / (V_b - V_o)

  I.e. 'the unknown resistor's value is equal to the known resistor's value multiplied by the voltage across the unknown resistor and divided by the difference of the bias voltage minus the voltage across the unknown resistor'.

  We can illustrate the way to find both resistors with a diagram:

  

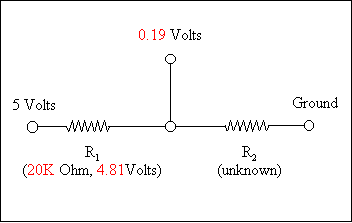
  If we run the equation for the above values (with V_i=5.00), we get:

  R2 = 20000 × 0.19v / (5.00 - .19v) R2 = 20000 × 0.19v / (4.81v) R2 = 3800 / 4.81v R2 = 790ohms

  We can also solve for an unknown R₁ (bias resistor) by changing the voltages around a little:

  R1 = 790 × 4.81v / (5.00 - 4.81v) R1 = 790 × 4.81v / (0.19v) R1 = 3800 / 0.19v R1 = 20000

  Note, the results aren't exactly as above, they are rounded.

• So, to find out what your bias resistor value is, follow this procedure:
  • Unplug the temp sensor and read its resistance, record this as R₂.
  • Plug the sensor back in and backprobe (insert paperclips or small diameter sharp probes into the silicone plug of the connector so that they are in electrical contact with the connector pins). NOTE: It's important that you DO NOT have the sensor unplugged while you have the ignition on. The computer may detect this as a failure and illuminate the Service light.
  • Next, turn on the ignition so that the computer is sending power to the sensor.
  • Now read the voltage across the sensor and record this as V_o.

• Now you have all the data you need to determine the bias resistor value.
  Bias Resistance (Ohms) = R₂ × (5 - V_o) / V_o

  So now you know what the bias value is.

  Here is a calculator for the bias resistor value:

  Supply Voltage (Vi):	Volts	Measured Voltage (Vo):	Volts	Sensor Resistance (R2):	quarts
  Bias Resistance (R1):

• To determine if your ECU switches the bias resistor during warmup, you need to perform the first test before the engine is hot, then stop the engine after it's run long enough to get to full temp, then perform the test again. If the bias resistor value you calculated is significantly different, your ECU switches them during temp sensor warmup.

• You then need to use EasyTherm (MS-I) or TunerStudio (MS-II+) to create a new thermistor table which uses the correct bias value. Use the bias resistor value you determined above, and three widely spaced temperature/resistance pairs (such as freezing, boiling, and another pair the middle) to burn a new table to the controller.